Эффект Даннинга-Крюгера — автокорреляция
Перевод статьи Блейра Фикса
Слышали ли вы об «эффекте Даннинга-Крюгера»? Это (кажущаяся) тенденция неквалифицированных людей переоценивать свою компетентность. Открытый в 1999 году психологами Джастином Крюгером и Дэвидом Даннингом, эффект с тех пор стал знаменитым
И вы поймёте, почему
Это одна из идей, которая настолько привлекательна, что не может не быть правдой. Всем же известно, что идиоты, как правило, не осознают своего идиотизма. Или, как выразился Джон Клиз:
Если вы очень очень глупы, как вы можете осознать, что вы очень очень очень глупы?
Конечно, психологи тщательно следят за тем, чтобы доказательства соответствовали научному критерию повторяемости. Но, как ни старайся, эффект Даннинга-Крюгера следует из данных. Поэтому теория кажется обоснованной
Но есть одна проблема
Эффект Даннинга-Крюгера проявляется даже в тех данных, в которых не должен. Например, если вы тщательно подберёте случайные данные, чтобы они не содержали эффекта Даннинга-Крюгера, вы всё равно обнаружите этот эффект. Причина оказывается досадно простой: эффект Даннинга-Крюгера не имеет никакого отношения к человеческой психологии.¹ Это статистический артефакт — потрясающий пример автокорреляции
Что такое автокорреляция?
Автокорреляция возникает, когда вы коррелируете переменную с самой собой. Например, если я измерю рост 10 человек, то обнаружу, что рост каждого из них отлично коррелирует с самим собой. Если это звучит как круговая логика, то так оно и есть. Автокорреляция — это статистический эквивалент утверждения 5 = 5
В такой формулировке идея автокорреляции звучит абсурдно. Ни один компетентный учёный не станет соотносить переменную с самой собой. И это справедливо для чистой автокорреляции. Но что, если переменная оказывается по обе стороны уравнения, и о ней забывают? В этом случае автокорреляцию обнаружить сложнее
Вот пример. Предположим, я работаю с двумя переменными: x и y. Я обнаружил, что эти переменные совершенно не коррелируют, как показано на левой панели рисунка 1. Пока всё хорошо
Далее я начинаю играть с данными. После некоторых манипуляций я получаю величину, которую называю z. Я сохраняю свою работу и забываю о ней. Спустя несколько месяцев мой коллега вновь обращается к моему набору данных и обнаруживает, что z сильно коррелирует с x (рис. 1, справа). Мы обнаружили что-то интересное!
На самом деле мы обнаружили автокорреляцию. Видите ли, без ведома моего коллеги я определил переменную z как сумму x + y. В результате, когда мы коррелируем z с x, мы фактически коррелируем x с самим собой. Переменная y сопутствует данным, обеспечивая статистический шум. Вот как происходит автокорреляция — забываешь, что по обе стороны корреляции находится одна и та же переменная
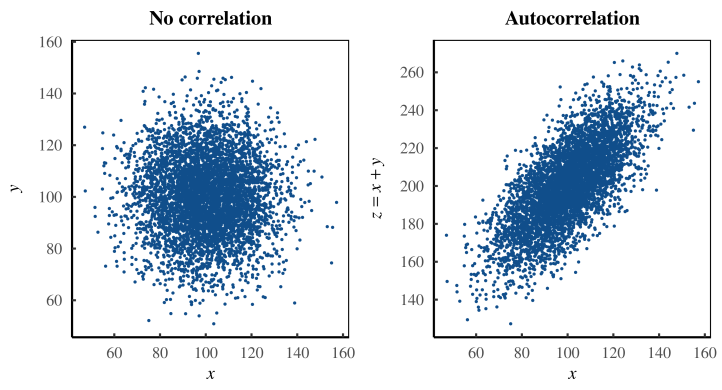
Рисунок 1: Создание автокорреляции. На левой панели изображены случайные величины x и y, которые не коррелируют между собой. На правой панели показано, как эта некоррелированность может быть преобразована в автокорреляцию. Мы определяем переменную z, которая сильно коррелирует с x. Проблема в том, что z — это сумма x + y. Таким образом, мы коррелируем x с самим собой. Переменная y добавляет статистический шум
Эффект Даннинга-Крюгера
Теперь, когда вы поняли, что такое автокорреляция, давайте поговорим об эффекте Даннинга-Крюгера. Как и в примере на рисунке 1, эффект Даннинга-Крюгера является автокорреляцией. Но вместо того, чтобы скрываться в переименованной переменной, автокорреляция Даннинга-Крюгера прячется под обманчивым графиком²
Давайте посмотрим
В 1999 году Даннинг и Крюгер сообщили о результатах простого эксперимента. Они попросили группу людей пройти тест на проверку навыков. (На самом деле, Даннинг и Крюгер провели несколько тестов, но это не имеет значения для моего обсуждения). Затем они попросили каждого человека оценить собственные способности. Даннинг и Крюгер (как им казалось) обнаружили, что люди, которые плохо справились с тестом, также были склонны переоценивать свои способности. Это и есть «эффект Даннинга-Крюгера»
Даннинг и Крюгер визуализировали свои результаты, как показано на рисунке 2. Это простая диаграмма, которая обращает внимание на разницу между двумя кривыми. По горизонтальной оси Даннинг и Крюгер распределили людей по четырем группам (квартилям) в соответствии с их результатами тестов. На диаграмме две линии демонстрируют результаты внутри каждой группы. Серая линия — средние результаты людей по тесту навыков. Чёрная линия — их среднее «восприятие собственных способностей». Очевидно, что люди, получившие низкие баллы по тесту навыков, слишком самоуверенны в оценке своих способностей (или так кажется)
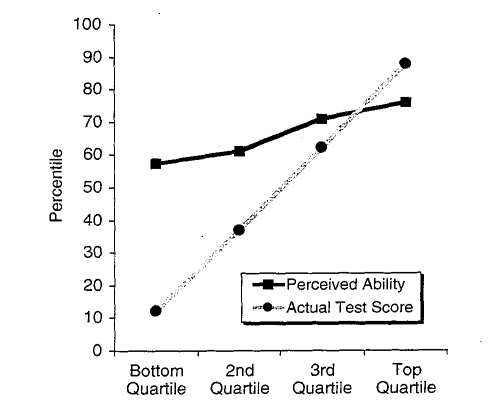
Рисунок 2: Диаграмма Даннинга-Крюгера. Из работы Даннинга и Крюгера (1999). На этом рисунке показано, как Даннинг и Крюгер сообщили о своих первоначальных результатах. Они провели тест на определение навыков, а также попросили каждого оценить свои способности. Затем распределили людей по четырем группам в соответствии с их рейтинговыми оценками по тесту. На этом рисунке показан контраст между средним процентилем «фактического тестового балла» в каждой группе (серая линия) и средним процентилем «оценки собственных способностей». Эффект Даннинга-Крюгера — это разница между двумя кривыми, то есть тот факт, что люди, не обладающие навыками, переоценивают свои способности
Сам по себе график Даннинга-Крюгера кажется убедительным. Добавьте к этому тот факт, что Даннинг и Крюгер — прекрасные авторы, и вы получите рецепт хитовой статьи. В связи с этим я рекомендую вам прочитать их статью, потому что она напоминает нам о том, что хорошая риторика — это не то же самое, что хорошая наука.
Деконструкция Даннинга-Крюгера
Теперь, когда вы увидели диаграмму Даннинга-Крюгера, давайте покажем, как она скрывает автокорреляцию. Чтобы всё было понятно, я буду комментировать графики по ходу дела
Начнём с горизонтальной оси. В диаграмме Даннинга-Крюгера горизонтальная ось является «категориальной», то есть показывает «категории», а не числовые значения. Конечно, нет ничего плохого в том, чтобы выделять категории. Но в данном случае категории на самом деле являются числовыми показателями. Даннинг и Крюгер берут результаты тестов людей и распределяют их по 4 ранжированным группам. В статистике эти группы называются «квартилями»
Это ранжирование означает, что по горизонтальной оси откладывается тестовый балл. Назовем этот балл x
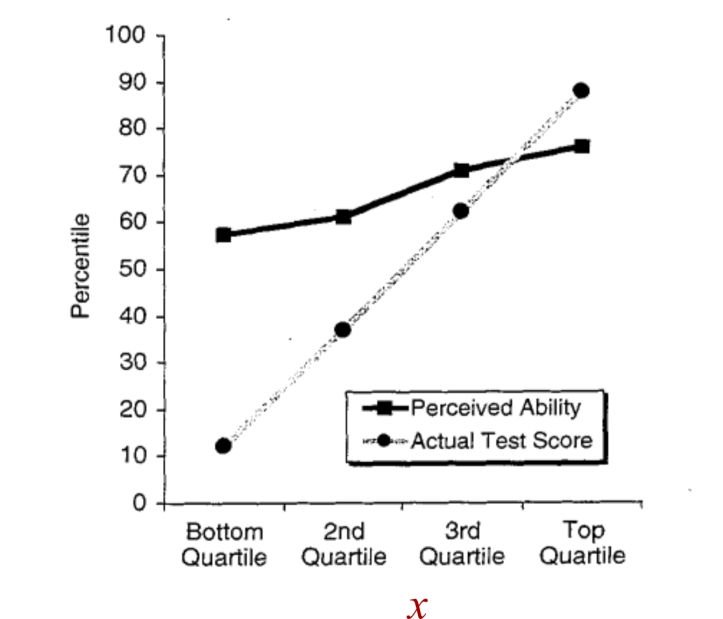
Рисунок 3: Деконструкция диаграммы Даннинга-Крюгера. На диаграмме Даннинга-Крюгера горизонтальная ось обозначает «фактический тестовый балл», который я назову x
Далее посмотрим на вертикальную ось, которая обозначена как «процентиль». Это означает, что вместо того, чтобы откладывать реальные результаты теста, Даннинг и Крюгер откладывают их рейтинг по 100-балльной шкале³
Теперь давайте посмотрим на кривые. Линия с надписью «фактический тестовый балл» показывает средний перцентиль тестового балла каждого квартиля (язык заплетается, я понимаю). Всё вроде бы хорошо, но до тех пор, пока мы не поймём, что Даннинг и Крюгер, по сути, строят график тестового балла (x) против него самого⁴. Заметив этот факт, давайте изменим обозначение серой линии. По сути, это график x против x
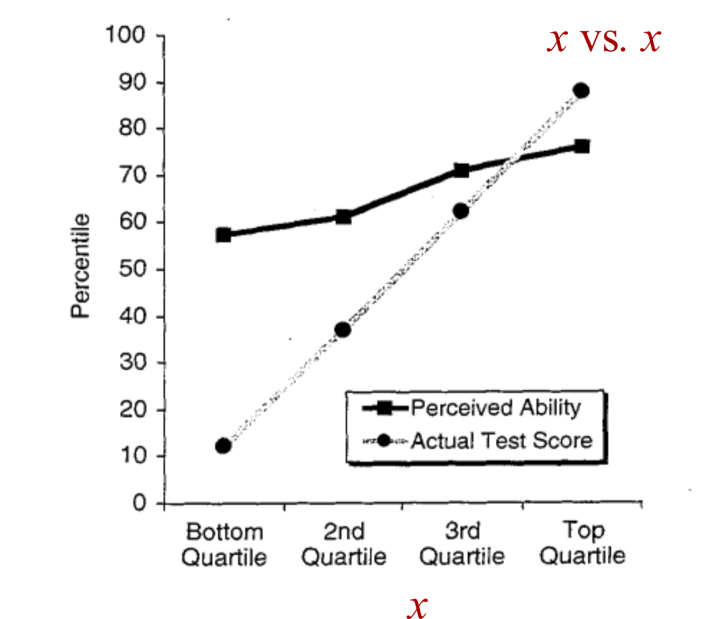
Рисунок 3: Деконструкция диаграммы Даннинга-Крюгера. На диаграмме Даннинга-Крюгера линия, обозначенная как «фактический результат теста», показывает результат теста (x) по отношению к самому себе. В моей системе обозначений это x против x
Двигаясь дальше, давайте посмотрим на график, обозначенный как «восприятие собственных способностей». Эта линия показывает средний процент самооценки каждой группы. Назовём эту самооценку y. Вспомнив, что мы обозначили «фактический результат теста» как x, мы увидим, что чёрная линия показывает отношение y к x
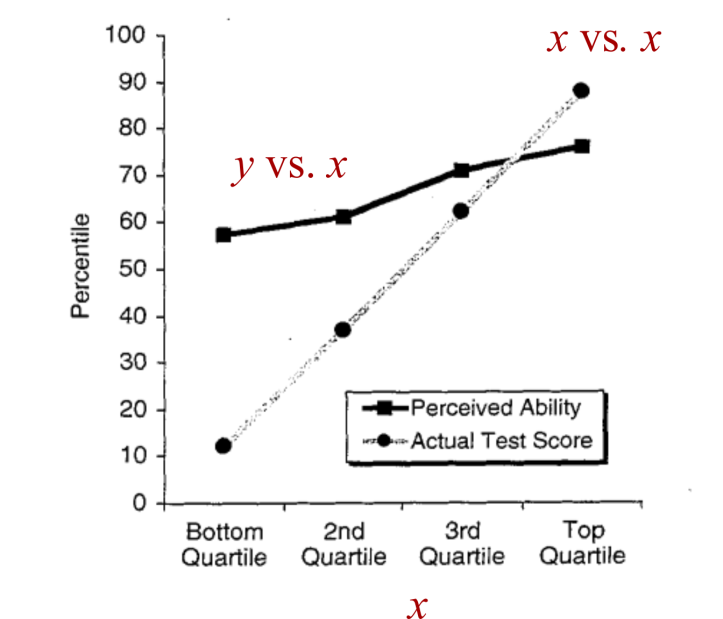
Рисунок 3: Деконструкция диаграммы Даннинга-Крюгера. На диаграмме Даннинга-Крюгера линия, обозначенная как «восприятие собственных способностей», строит график «воспринимаемых способностей» y против реального тестового балла x
Пока что ничего не бросается в глаза как явная ошибка. Да, это немного странно — строить график x против x. Но Даннинг и Крюгер не утверждают, что важна только эта линия. Важна разница между двумя линиями («восприятия собственных способностей» и «реальных результатов теста»). Именно в этой разнице и проявляется автокорреляция
В математических терминах «разница» означает «вычесть». Поэтому, показывая нам две расходящиеся линии, Даннинг и Крюгер (неявно) просят нас вычесть одну из другой: возьмите «восприятие собственных способностей» и вычтите «фактический тестовый балл». В моей системе обозначений это соответствует y — x
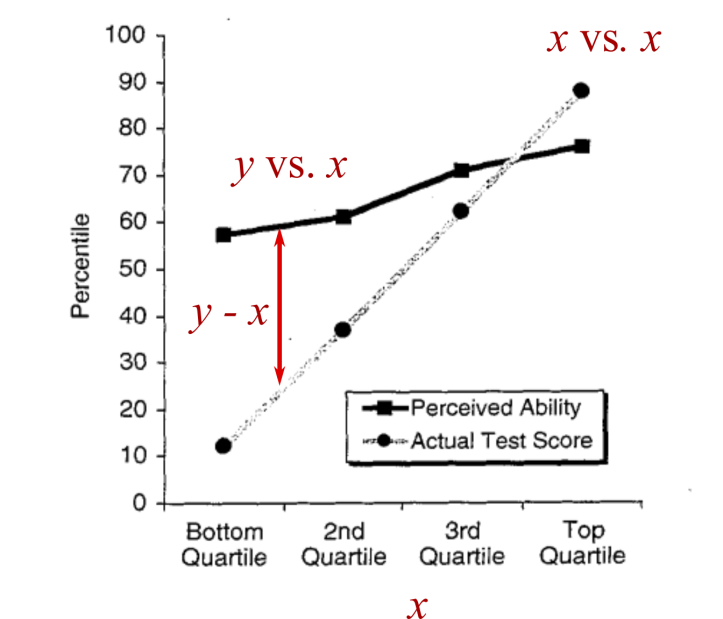
Рисунок 3: Деконструкция диаграммы Даннинга-Крюгера. Чтобы интерпретировать график Даннинга-Крюгера, мы (неявно) смотрим на разницу между двумя кривыми. Это соответствует тому, чтобы взять «восприятие собственных способностей» и вычесть из него «фактический тестовый балл». В моей системе обозначений эта разница равна y — x (обозначена двунаправленной стрелкой). Когда мы оцениваем эту разницу как функцию горизонтальной оси, мы неявно сравниваем y — x с x. Поскольку x находится по обе стороны сравнения, результатом будет автокорреляция
Вычитание y — x кажется нормальным, пока мы не поймём, что должны интерпретировать эту разницу как функцию горизонтальной оси. Но по горизонтальной оси откладывается тестовый балл x. Поэтому нас (неявно) просят сравнить y — x с x:
(y — x) ∼ x
Видите, в чём проблема? Мы сравниваем x с отрицательной версией самого себя. Это хрестоматийная автокорреляция. Это значит, что мы можем подставлять вместо x и y случайные числа — числа, которые не могут содержать эффект Даннинга-Крюгера — и всё равно эффект проявится
Воспроизведение Даннинга-Крюгера
Честно говоря, меня не особо убеждают приведённые выше аналитические аргументы. Только используя реальные данные я могу понять проблему с эффектом Даннинга-Крюгера. Так что давайте посмотрим на реальные числа
Предположим, что мы — психологи, получившие большой грант на воспроизведение эксперимента Даннинга-Крюгера. Мы набираем 1000 человек, проводим с каждым из них тест на определение навыков и просим их дать оценку своих способностей. Получив результаты, мы смотрим на данные
Они выглядят не очень хорошо
Если мы сравним результаты теста с самооценкой, данные будут выглядеть совершенно случайными. На рисунке 7 показано это распределение. Похоже, что люди вне зависимости от навыков одинаково плохо оценивают свои способности. Здесь нет и намёка на эффект Даннинга-Крюгера
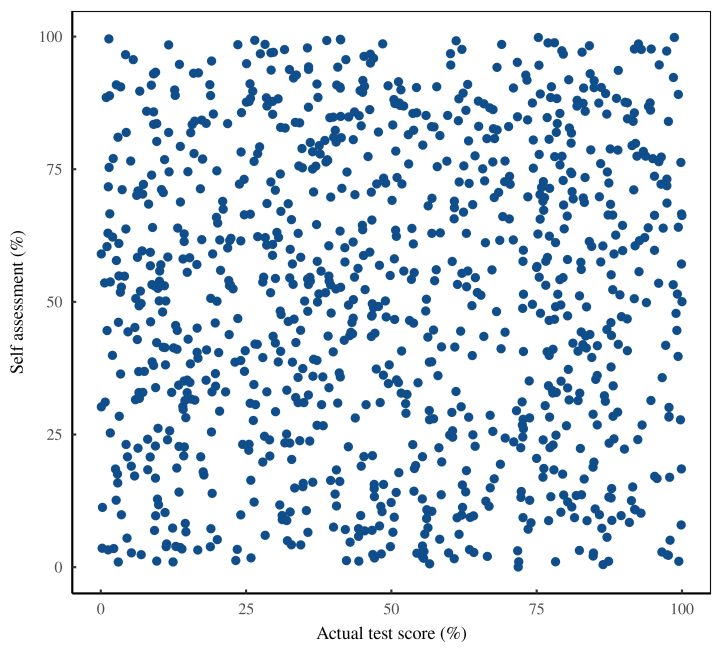
Рисунок 7: Неудачная репликация. На этом рисунке показаны результаты мысленного эксперимента, в котором мы пытаемся воспроизвести эффект Даннинга-Крюгера. Мы попросили 1000 человек пройти тест на определение навыков и оценить свои способности. Здесь представлены исходные данные. Каждая точка представляет собой результат отдельного человека: по горизонтали — «фактический результат теста», по вертикали — «самооценка». Здесь нет и намёка на эффект Даннинга-Крюгера
Посмотрев на исходные данные, мы забеспокоились, что сделали что-то не так. Множество других исследователей воспроизвело эффект Даннинга-Крюгера. Неужели мы допустили ошибку в нашем эксперименте?
К сожалению, мы не можем собрать больше данных (у нас закончились деньги). Но мы можем поиграться с анализом. Коллега предлагает вместо построения графика исходных данных вычислить «ошибку самооценки» каждого человека. Эта ошибка — разница между самооценкой человека и его тестовым баллом. Возможно, эта ошибка оценки связана с реальным результатом теста?
Мы проводим расчёты и, к нашему изумлению, обнаруживаем огромный эффект. Результаты — на рисунке 8. Похоже, что неквалифицированные люди чрезвычайно самоуверенны, а квалифицированные — чрезмерно скромны
(Наши лаборанты отмечают, что корреляция удивительно чёткая, как будто числа подбирались вручную. Но мы игнорируем это замечание и продолжаем работать дальше)
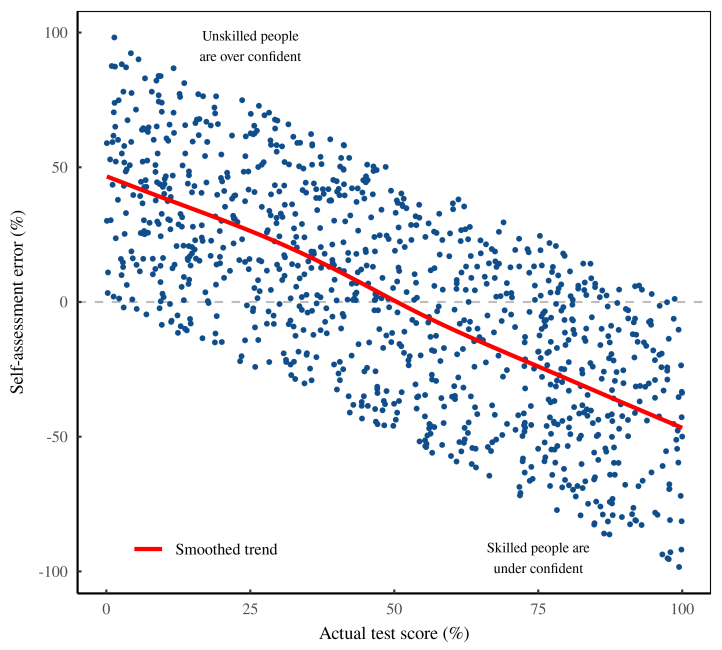
Рисунок 8: Может быть, эксперимент был успешным? Используя исходные данные с рисунка 7, мы рассчитали «ошибку самооценки» — разницу между самооценкой человека и его реальными тестовыми баллами. Эта ошибка оценки (вертикальная ось) сильно коррелирует с фактическим результатом теста (горизонтальная ось)
Воодушевленные успехом на рисунке 8, мы решаем, что результаты, возможно, не так уж и плохи. Поэтому мы бросаем данные в диаграмму Даннинга-Крюгера, чтобы посмотреть, что получится. Мы обнаруживаем, что, несмотря на наши опасения по поводу данных, эффект Даннинга-Крюгера присутствовал всегда. На самом деле, как показывает рисунок 9, наш эффект даже больше, чем на исходной диаграмме с рисунка 2
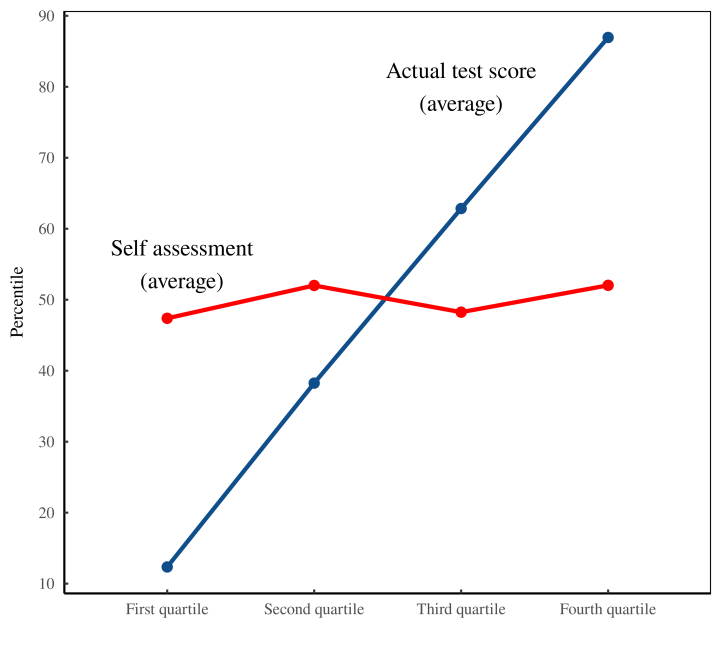
Рисунок 9: Вос Даннинга и Крюгера. Несмотря на кажущееся отсутствие эффекта в наших исходных данных (рисунок 7), когда мы подставляем эти данные в диаграмму Даннинга-Крюгера, мы обнаруживаем явный эффект. Неквалифицированные люди переоценивают свои способности, а опытные — слишком скромны
Всё рушится
Довольные успешным воспроизведением эксперимента, мы начинаем записывать результаты. И тут всё рушится. Хранитель наших данных, испытывая чувство вины, всё же сознаётся: он потерял данные нашего эксперимента и в приступе паники заменил их случайными числами. Наши результаты, признаётся он, основаны на статистическом шуме
Опустошённые, мы возвращаемся к нашим данным, чтобы понять, что пошло не так. Если мы работали со случайными числами, то как мы могли воспроизвести эффект Даннинга-Крюгера? Чтобы понять, что произошло, отбросим притворство, что мы работаем с психологическими данными. Мы перемаркируем наши графики абстрактными переменными x и y. Сделав это, мы обнаруживаем, что наш «эффект» на самом деле является автокорреляцией
На рисунке 10 это показано наглядно. Наш набор данных состоит из статистического шума — двух случайных переменных x и y, которые совершенно не связаны между собой (диаграмма A). Когда мы рассчитывали «ошибку самооценки», мы взяли разницу между y и x. Неудивительно, что эта разница коррелирует с x (диаграмма B). Всё дело в том, что x автокоррелирует с самим собой. Наконец, мы разбираем диаграмму Даннинга-Крюгера и понимаем, что она тоже основана на автокорреляции (диаграмма C). Она просит нас интерпретировать разницу между y и x как функцию от x. Это автокорреляция из диаграммы B, обёрнутая в более обманчивую обёртку
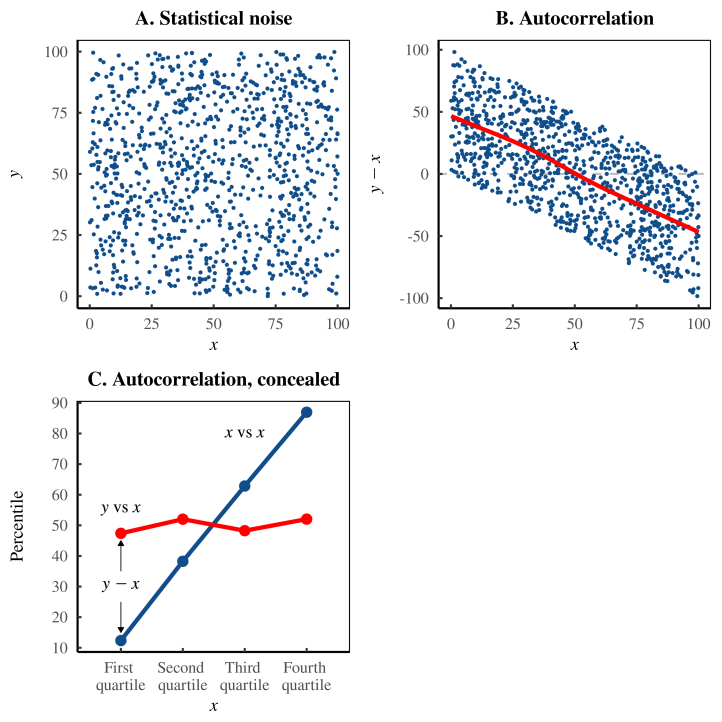
Рисунок 10: Отказ от психологических притязаний. Этот рисунок повторяет анализ, показанный на рисунках 7—9, но отбрасывает претензию на то, что мы имеем дело с психологией человека. Мы работаем со случайными переменными x и y, взятыми из равномерного распределения. На диаграмме A показано, что переменные совершенно не коррелируют между собой. На диаграмме B показано, что когда мы строим график y — x против x, мы получаем сильную корреляцию. Но это потому, что мы скоррелировали x с самим собой. На панели C мы вводим эти переменные в диаграмму Даннинга-Крюгера. И снова кажущийся эффект является автокорреляцией — интерпретацией y — x как функции от x
Смысл этой истории в том, чтобы проиллюстрировать, что эффект Даннинга-Крюгера не имеет ничего общего с человеческой психологией. Это статистический артефакт — пример автокорреляции, скрывающейся на виду
Интересно то, сколько времени потребовалось исследователям, чтобы обнаружить ошибку в анализе Даннинга и Крюгера. Даннинг и Крюгер опубликовали свои результаты в 1999 году. Но ошибку не замечали вплоть до 2016 года. Насколько мне известно, Эдвард Нюфер и его коллеги были первыми, кто исчерпывающе развенчал эффект Даннинга-Крюгера (см. их совместные работы, опубликованные в 2016 и 2017 годах). В 2020 году Жиль Жиньяк и Марцин Заенковски опубликовали аналогичную критику
После прочтения этих критических статей становится до боли очевидно, что эффект Даннинга-Крюгера — всего лишь статистический артефакт. Но до сих пор мало кто знает об этом факте. В три критические статьи в сумме имеют примерно в 90 раз меньше цитирований, чем оригинальная статья Даннинга-Крюгера⁵. Поэтому есть подозрение, что большинство учёных по-прежнему считают, что эффект Даннинга-Крюгера — это устойчивый аспект человеческой психологии
Никаких признаков Даннинга-Крюгера
Проблема с диаграммой Даннинга-Крюгера заключается в том, что она нарушает фундаментальный принцип статистики. Если вы собираетесь соотнести два набора данных, они должны быть собраны независимо друг от друга. В диаграмме Даннинга-Крюгера этот принцип нарушается. Диаграмма помещает результаты тестов на обе оси, что приводит к автокорреляции
Осознав эту ошибку, Эдвард Нюфер и его коллеги задались интересным вопросом: что произойдёт с эффектом Даннинга-Крюгера, если измерить его статистически достоверным способом? Согласно полученным Нюфером данным, ответ заключается в том, что эффект исчезает.
На рисунке 11 показаны их результаты. Здесь важно то, что «навык» людей измеряется независимо от результатов их тестов и самооценки. Чтобы измерить «навыки», Нюфер группирует людей по уровню их образования, показанному по горизонтальной оси. По вертикальной оси откладывается расхождение с самооценкой людей. Каждая точка представляет собой отдельного человека
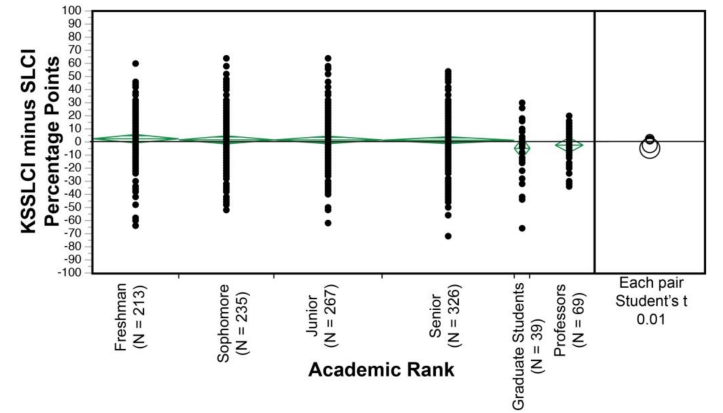
Рисунок 11: Статистически достоверный тест на эффект Даннинга-Крюгера. На этом рисунке показан тест эффекта Даннинга-Крюгера, проведённый Нюфером и его коллегами в 2017 году. Как и на рисунке 8, на этой диаграмме отображается соотношение навыков людей и их ошибки в самооценке. Но, в отличие от рисунка 8, здесь переменные статистически независимы. По горизонтальной оси навык измеряется с помощью академического ранга. Вертикальная ось измеряет ошибку самооценки следующим образом. Нухфер берёт баллы человека по тесту SLCI (science literacy concept inventory test) и вычитает их из его самооценки, которая называется KSSLCI (knowledge survey of the SLCI test). Каждая чёрная точка обозначает ошибку в самооценке человека. Зелёным цветом указаны средние значения в каждой группе с соответствующим доверительным интервалом. Тот факт, что зелёные линии перекрывают линию нулевого эффекта, указывает на то, что внутри каждой группы средние значения статистически не отличаются от 0. Другими словами, нет никаких признаков эффекта Даннинга-Крюгера
Если бы эффект Даннинга-Крюгера присутствовал, он проявился бы на рисунке 11 в виде тенденции к снижению данных (аналогично тенденции на рисунке 7). Такая тенденция свидетельствовала бы о том, что неквалифицированные люди действительно переоценивают свои способности, и что эта «самоуверенность» уменьшается с ростом квалификации. Если посмотреть на рисунок 11, то здесь нет и намёка на тенденцию. Вместо этого средняя ошибка в оценке (обозначенная зелёным цветом) колеблется около нуля. Другими словами, погрешность оценки тривиально мала
Несмотря на отсутствие эффекта Даннинга-Крюгера, на рисунке 11 прослеживается интересная закономерность. Если двигаться слева направо, то разброс ошибок в самооценке имеет тенденцию к уменьшению с ростом уровня образования. Другими словами, профессора в целом лучше оценивают свои способности, чем первокурсники. Это вполне логично. Заметьте, однако, что это увеличение точности отличается от эффекта Даннинга-Крюгера, который заключается в систематической предвзятости средней оценки. В данных Нюфера такой предвзятости не наблюдается
Неквалифицированные и несведущие
Ошибки случаются. Поэтому мы не можем обвинять Даннинга и Крюгера в том, что они ошиблись. Однако, в обстоятельствах их ошибки есть восхитительная ирония. Вот два профессора Лиги плюща⁷ утверждают, что неквалифицированные люди несут «двойное бремя»: неквалифицированные люди не просто «некомпетентны», но и не осознают своей некомпетентности
Ирония заключается в том, что на самом деле ситуация обратная. В своей основополагающей работе Даннинг и Крюгер именно транслируют свою (статистическую) некомпетентность, путая автокорреляцию с психологическим эффектом. В этом свете название работы, возможно, всё ещё уместно. Просто авторы (а не испытуемые) были «некомпетентны и не знали об этом»
Примечания:
- Эффект Даннинга-Крюгера ничего не говорит нам о людях, которых он якобы измеряет. Но он говорит нам о психологии социологов, которые, очевидно, испытывают трудности со статистикой
- Кажется очевидным, что Даннинг и Крюгер не хотели никого обманывать. Вместо этого, похоже, они обманули себя (и многих других). В этой связи мне стыдно признаться, что я прочитал статью Даннинга и Крюгера несколько лет назад и не заметил ничего плохого. Только после прочтения статьи Джонатана Джерри я понял, в чём дело. Это немного неловко, ведь одной из главных тем этого блога было то, что я указывал на то, как экономисты апеллируют к автокорреляции при проверке своих теорий стоимости. (Примеры здесь, здесь, здесь, здесь и здесь). Я утешаюсь тем, что многие учёные тоже были одурачены таблицей Даннинга-Крюгера ︎п︎одобным образом
- Преобразование в процентили вносит вторую погрешность (в дополнение к проблеме автокорреляции). По определению, перцентили имеют дно (0) и потолок (100) и равномерно распределены между этими границами. Если вы находитесь близко к полу, то занизить свой ранг невозможно. Поэтому «некомпетентные» будут выглядеть слишком самоуверенными. А если вы находитесь близко к потолку, то переоценить свой ранг невозможно. Поэтому «опытные» будут казаться слишком скромными. Подробнее см. в работе Нюфера (2016)
- С технической точки зрения, Даннинг и Крюгер строят график двух различных форм ранжирования друг против друга — «процентиль» тестового балла против «квартиля» тестового балла. Что не очевидно, так это то, что этот тип графика является *независимым от данных*. По определению, каждый квартиль содержит 25 перцентилей, среднее значение которых соответствует медиане квартиля. Следствием этой банальности является то, что график «фактического тестового балла» ничего не говорит нам (как это ни парадоксально) о фактических тестовых баллах людей
- По данным Google scholar, три критические статьи (Nuhfer 2016, 2017 и Gignac and Zajenkowski 2020) имеют 88 цитирований в совокупности. Для сравнения, Даннинг и Крюгер (1999) имеют 7893 цитирования
- Медленное распространение «разоблачений» — распространённая проблема в науке. Даже когда оригинальные (ошибочные) статьи опровергаются, они часто продолжают собирать цитирования. Кроме того, критические статьи редко публикуются в том же журнале, в котором была опубликована оригинальная статья. Так что небезупречная статья в *Nature*, скорее всего, будет развенчана в более малоизвестном журнале. Эта асимметрия отчасти объясняет, почему я пишу здесь об эффекте Даннинга-Крюгера. Я думаю, что критика, поднятая Нюфером и др. (Жиньяком и Заенковски), заслуживает широкой известности
- Когда Даннинг и Крюгер опубликовали свою работу 1999 года, они оба работали в Корнельском университете
Дополнительная литература:
Gignac, G. E., & Zajenkowski, M. (2020). The Dunning-Kruger effect is (mostly) a statistical artefact: Valid approaches to testing the hypothesis with individual differences data. Intelligence, 80, 101449.
Kruger, J., & Dunning, D. (1999). Unskilled and unaware of it: How difficulties in recognizing one’s own incompetence lead to inflated self-assessments. Journal of Personality and Social Psychology, 77(6), 1121.
Nuhfer, E., Cogan, C., Fleisher, S., Gaze, E., & Wirth, K. (2016). Random number simulations reveal how random noise affects the measurements and graphical portrayals of self-assessed competency. Numeracy: Advancing Education in Quantitative Literacy, 9(1).
Nuhfer, E., Fleisher, S., Cogan, C., Wirth, K., & Gaze, E. (2017). How random noise and a graphical convention subverted behavioral scientists’ explanations of self-assessment data: Numeracy underlies better alternatives. Numeracy: Advancing Education in Quantitative Literacy, 10(1).

.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)

.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)

.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)
.jpeg)