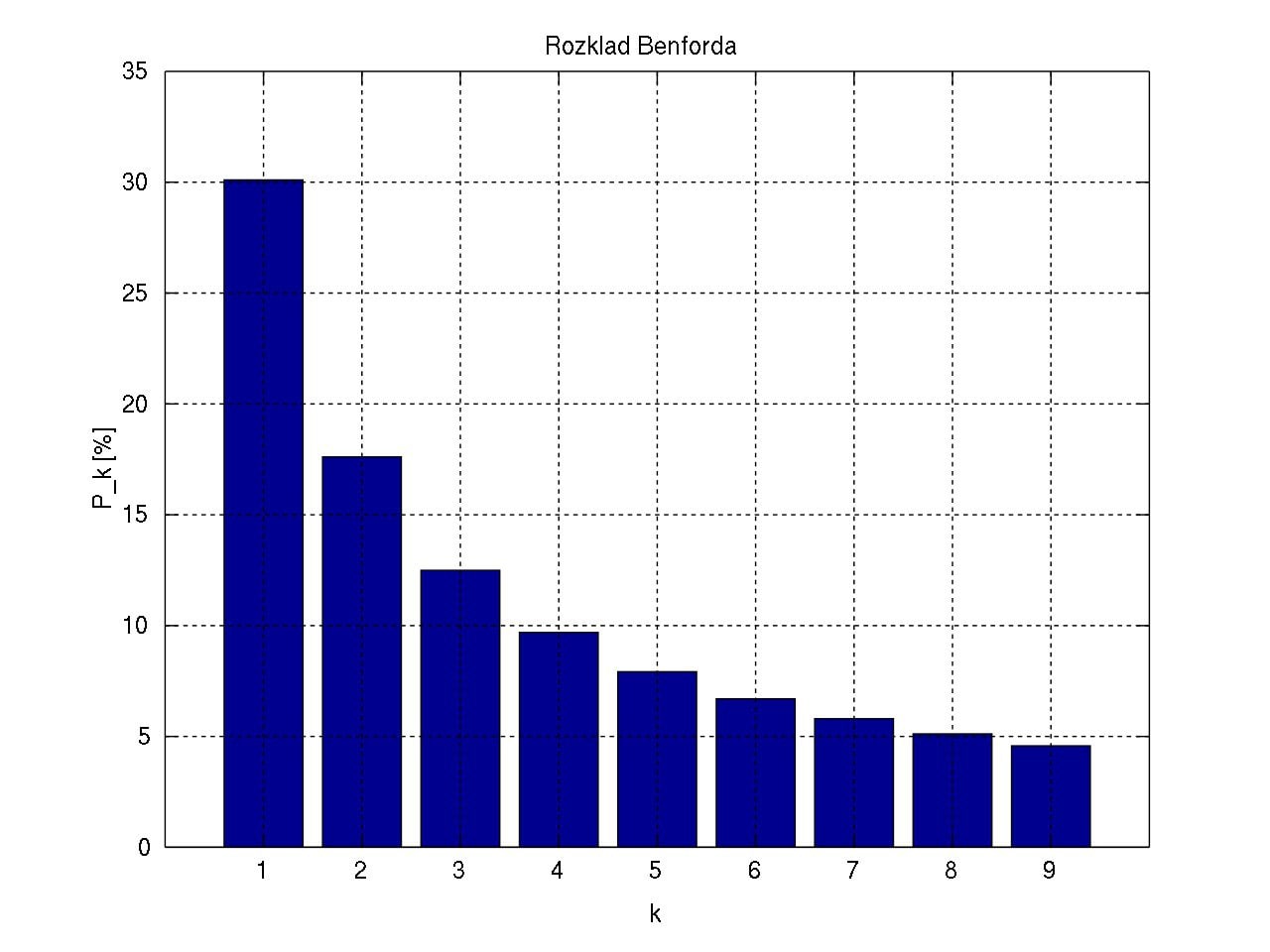
Этот закон описывает то, как часто цифры будут первыми в числах из большого массива значений в реальной жизни. Например, единица в 6 раз чаще восьмёрки будет встречаться в начале чисел, что показано на первой диаграмме. По горизонтали — первые значащие цифры, по вертикали — вероятность их появления

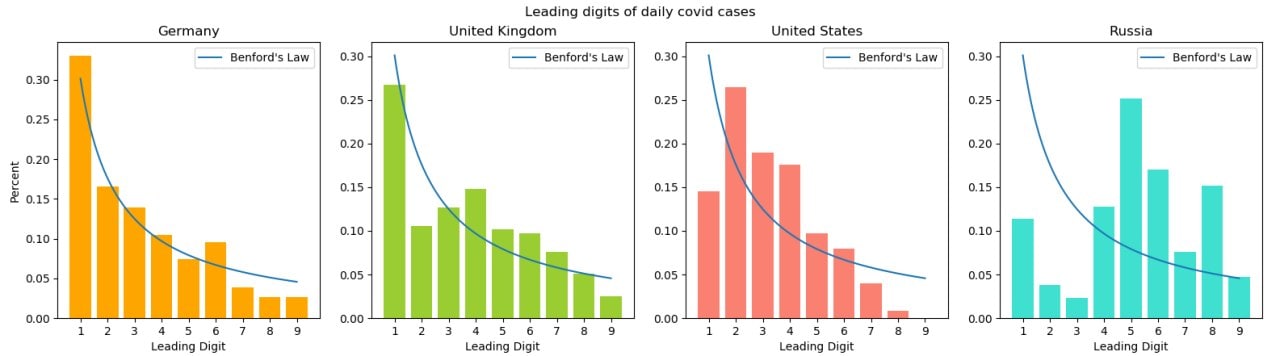
Контринтуитивность закона позволяет выявлять мошенничества с финансами, фальсификации на выборах или подтасовки статистики. Если распределение цифр в массиве данных значительно отличается от распределения Бенфорда — числа с большой вероятностью имели искусственную природу. Например, при помощи этого закона пользователь с Reddit указал на подтасовки в данных о заболеваемости короной в России. На третьем изображении — его визуализация распределения цифр в количестве новых заболеваний коронавирусом в Германии, Великобритании, США и России

Необходимо понимать, что закон верен не для всех распределений. Он не работает, если заданы минимальные и максимальные значения или у величин только один или два порядка значений. Например, распределение цифр в списке компаний с доходом от 50 тыс до 100 тыс $ или показатели IQ у взрослых не будут под него подходить

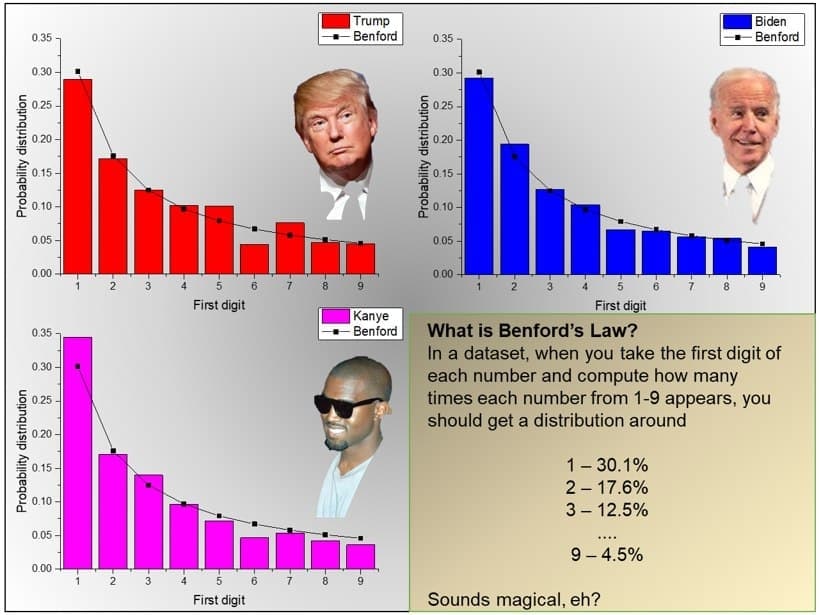
В последнем вложении — распределение цифр в числе голосов, поданных за кандидатов на президентских выборах в США, по округам