Измерение неравенства: что такое коэффициент Джини?
Коэффициент Джини является наиболее распространённым показателем неравенства. Но что он на самом деле измеряет? И чем он отличается от других показателей неравенства?
Коэффициент Джини, или индекс Джини, является наиболее распространённым показателем неравенства. Он был разработан итальянским статистиком Коррадо Джини (1884—1965 гг.) и назван в его честь
Обычно он используется для измерения неравенства доходов, но также может применяться для измерения неравенства любого распределения — распределения богатства или даже ожидаемой продолжительности жизни
Неравенство измеряется по шкале от 0 до 1, где более высокие значения указывают на более высокий уровень неравенства. Иногда этот показатель может быть представлен в процентах от 0 до 100%, тогда он называется «индексом Джини»
Значение 0 означает полное равенство, когда все имеют одинаковый доход. Значение 1 означает полное неравенство, когда один человек получает весь доход, а все остальные — ничего
Как рассчитывается коэффициент Джини?
Существует два основных способа расчёта коэффициента Джини. Оба приводят к одним и тем же значениям, но дают нам два представления о том, что именно измеряет коэффициент
Метод 1: Расчёт разницы между доходами двух человек по отношению к среднему значению
Первый метод можно проиллюстрировать следующим мысленным экспериментом
Представьте двух людей, случайно столкнувшихся на улице. Они сравнивают свои доходы и выясняют, насколько один из них богаче другого. Насколько большую разницу можно ожидать?
Этот ожидаемый разрыв между двумя случайно выбранными людьми и измеряется коэффициентом Джини. Он рассчитывается как среднее значение разрыва между всеми парами людей в населении
Если доходы распределены равномерно, то можно ожидать небольшой разрыв между доходами двух случайно выбранных людей. Там, где высокий уровень неравенства, мы можем ожидать большой разрыв
Однако, если измерять этот показатель в абсолютном выражении, он также будет зависеть от богатства населения в целом. Если даже самые обеспеченные представители населения имеют низкий доход, то абсолютный разрыв между доходами людей будет маленьким. И наоборот — там, где доходы в целом высоки, даже небольшая относительная разница (напрмер, в %) будет означать большой разрыв в абсолютных показателях
По этой причине коэффициент Джини учитывает также средний доход среди населения
В частности, он рассчитывается как ожидаемый разрыв в пределах удвоенного среднего дохода. Для простоты представим, что всё население состоит из тех двух человек, встретившихся на улице. Если их общий доход составляет 100 $, то средний по населению будет 50 $. Если доход первого составляет 100 $, а второго — 0 $, разница в доходах будет равна 100 $, что как раз в два раза больше среднего уровня дохода
Таким образом, наибольшее возможное значение среднего разрыва, то есть удвоенный средний доход — ситуация абсолютного неравенства. Все доходы принадлежат одному человеку, а остальные вовсе не имеют дохода — коэффициент Джини равен 1
Наименьшее возможное значение среднего разрыва, то есть 0 — ситуация абсолютного равенства. Доходы всех людей равны — коэффициент Джини равен 0
Метод 2: Разрыв между «кривой Лоренца» и «линией идеального равенства»
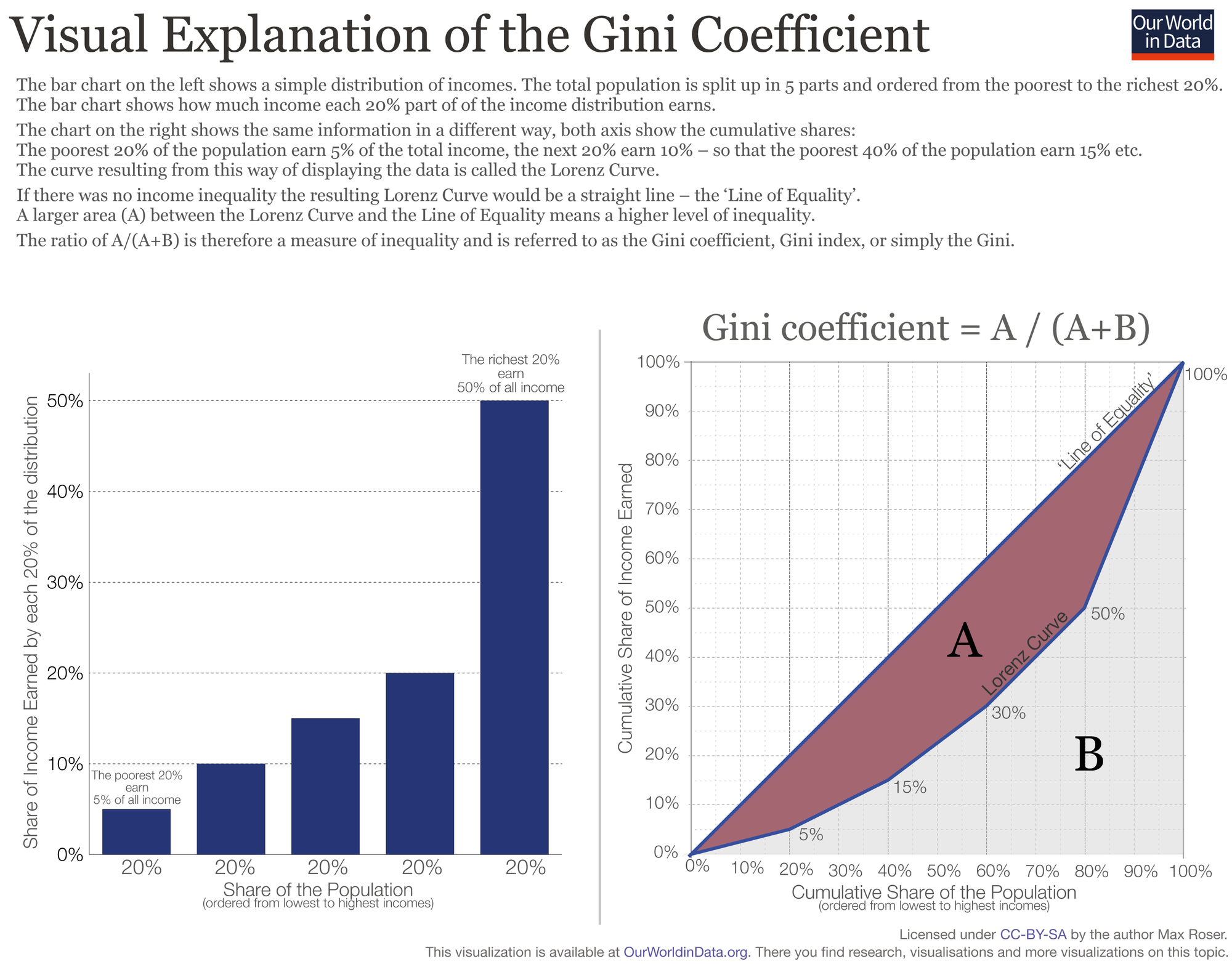
Слева указана доля дохода, получаемая каждой пятой частью гипотетического населения. Справа — суммарные доходы всех групп населения. Получившийся справа график называется «кривой Лоренца»
Для населения, среди которого доходы распределены абсолютно равномерно, «кривая Лоренца» будет представлять собой прямую диагональную линию: 10% самых бедных будут получать 10% от общего дохода, 20% — 20% от общего дохода и т. д. Это показано на графике как «линия равенства»
Но среди населения, представленного на нашей диаграмме, доходы распределяются неравномерно. 60% населения с наименьшим доходом получает 30% от общего дохода
Коэффициент Джини показывает, насколько «кривая Лоренца» отклоняется от «линии равенства», сравнивая площади A и B на картинке. Отклонение рассчитывается следующим образом:
коэффициент Джини = A ÷ (A + B)
Если доходы распределяются абсолютно равномерно, «кривая Лоренца» будет совпадать с «линией равенства». Площадь A, как и коэффициент Джини, будет равна 0. Если один человек получает все доходы, а остальные не имеют никакого, «кривая Лоренца» совпадает с осью X — общие доходы будут сконцентрированы в конце графика. Площадь B будет равна нулю, а коэффициент Джини — 1
Сравнение показателей: Рассказывает ли показатель Джини ту же историю, что и другие показатели неравенства?
Показатели неравенства пытаются обобщить информацию о том, насколько распределение неравномерно — точно так же, как стандартное отклонение. В таких суммарных показателях заложены суждения о том, что именно должно иметь наибольшее значение при измерении неравенства
Для примера сравним два выдуманных общества. В первом богатые люди намного богаче тех, кто находится в середине распределения, но доходы более бедных лишь немного ниже тех, что получают в середине. Во втором — обратная ситуация: доходы богатых лишь немного выше доходов средних, но бедные намного беднее
В каком обществе выше неравенство? Ответ будет зависеть от того, какие разрывы в разных частях распределения считать вносящими наибольший вклад в уровень неравенства. Такие оценочные суждения неявно заложены в математические определения показателя неравенства
Это относится ко всем показателям неравенства, и коэффициент Джини не является исключением. Но его отличает более высокая чувствительность к изменениям в середине распределения, чем в самом верху и внизу
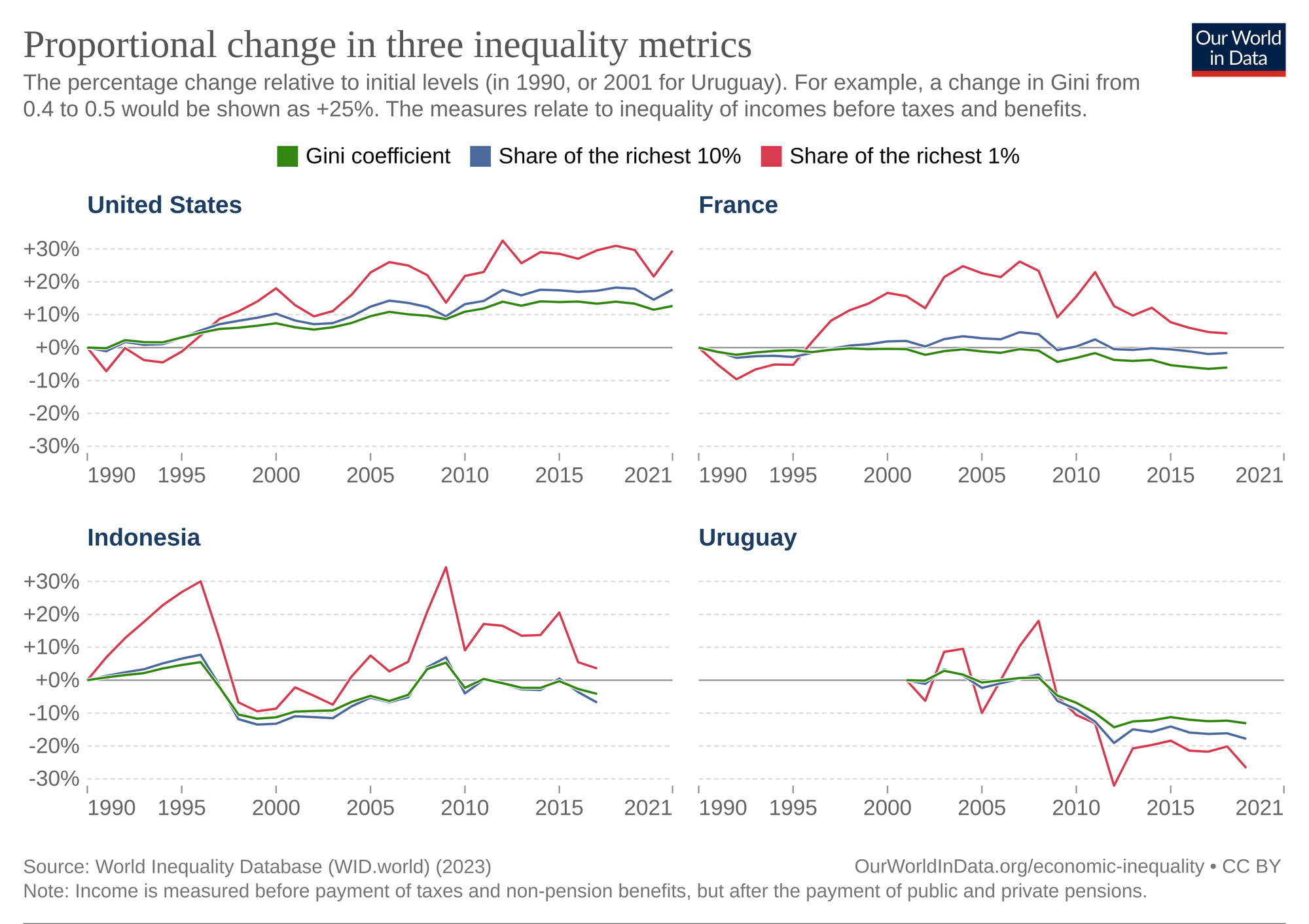
Особенности коэффициента Джини можно рассмотреть на примере четырёх стран. На диаграммах показано, как он соотносится с двумя другими показателями неравенства — долями дохода 1% и 10% самого богатого населения. Для наглядности приведена динамика с течением времени. По вертикали — разница в % относительно показателей 1900 года
Мы видим, что существенное изменение доли доходов 1% самых богатых сопровождается незначительным изменением коэффициента Джини. Это справедливо как для стран с растущим уровнем неравенства (США), так и для стран, где уровень неравенства снижается (Уругвай)
В то же время, коэффициент Джини гораздо точнее отслеживает долю доходов самых богатых 10%. Коэффициент Джини не чувствителен к изменениям только в самой верхней части распределения
Источник — Our World in Data
