Тег: математика

Гипотеза Коллатца — одна из нерешённых проблем математики, сформулированная 1 июля 1932 года. Она заключается в том, что при любом натуральном числе
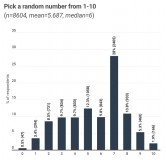
Я уже писал о сложностях с рандомом у людей. Вот ещё одно свидетельство того, что мы не сильны в генерации случайных чисел и последовательностей
Есть такой контринтуитивный закон Бенфорда или закон первой цифры см. этот пост. Если очень упрощённо, то в природе существуют такие наборы случайных данных
Насколько большими вообще бывают числа? Вот несколько примеров очень-очень больших чисел
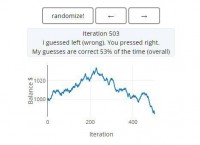
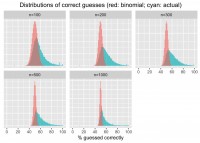
Похоже, что нет. Ваши пальцы имеют тенденцию повторять определённые рисунки, даже если вы этого не замечаете
Компьютер американского инженера Джонатана Пейса нашел 50-е простое число Мерсенна — 2^77232917-1. Оно содержит 23 249 425 цифр